SwissBorg: Proof-of-Liabilities

An wen richtet sich dieser Bericht?

Leser: Jeden

Technisches Niveau: Mittel

Vorkenntnisse: Gewisse Kenntnisse über Kryptographie. Kenntnisse der aktuellen Informatik.

Dieses Dokument richtet sich an einen möglichst breiten Leserkreis. Dennoch handelt es sich um eine technische Erläuterung von Rechenprozessen, die dem Leser ein gewisses Maß an Kenntnissen der Informatik und der Kryptographie abverlangt, um die Materie vollständig zu verstehen.

Einführung

Die jüngsten Ereignisse im Bereich der Kryptowährungen haben deutlich gemacht, dass die Öffentlichkeit ein Recht darauf hat, sicher zu sein, dass ihre Guthaben sicher, geprüft und zugänglich sind..

Im Rahmen unserer Transparenz-Initiative "Wir vertrauen auf SwissBorg" möchten wir die Einführung des SwissBorg Proof-of-Liabilities-Portals ankündigen, einer Web-Reporting-Lösung, die es unseren Nutzern ermöglicht, ihre Guthaben einzusehen und sicherzustellen, dass ihre Guthaben in der Gesamtsumme berücksichtigt werden.

Ein Proof-of-Liabilities-Protokoll zeigt im Wesentlichen die Gesamtverbindlichkeiten der Nutzer an und ermöglicht es jedem Nutzer zu überprüfen, ob seine Verbindlichkeiten in der Gesamtsumme berücksichtigt sind, um nachweisen zu können, dass seine Verbindlichkeiten in der Gesamtsumme nicht weggelassen oder reduziert wurden.

Im Einklang mit der gemeinschaftsorientierten Philosophie von SwissBorg ist es seit langem eine Voraussetzung, dass unsere Nutzer selbst überprüfen können, ob ihre Verbindlichkeiten in unserem PoL enthalten sind, ohne dass sie sich auf einen externen Prüfer verlassen müssen. Die Vereinfachung dieses Überprüfungsprozesses für die Nutzer war ein wesentlicher Bestandteil des PoL-Validierungsmechanismus.

Auf der Suche nach der richtigen Lösung hat das Entwicklungsteam von SwissBorg einen PoL-Verifizierungsmechanismus entwickelt, der auf dem bewährten kryptografischen Hash Tree-Verfahren basiert und eine solide und bekannte technische Grundlage bietet, auf der wir aufbauen können.

Was die Implementierung betrifft, so haben wir uns für eine webbasierte Lösung entschieden, bei der der Browser die Verbindlichkeiten des Nutzers validiert, so dass der Validierungsprozess für jeden, der den Code und die Daten sehen und überprüfen möchte, völlig transparent ist.

Wir sind der Meinung, dass unsere PoL-Lösung durch die Verwendung dieser robusten und zuverlässigen Validierungs- und Implementierungsmethoden Ansätze zur Selbstverifizierung und reibungslosen Nutzerfreundlichkeit auf bestmögliche Weise kombiniert.

Dieser Artikel erläutert das kryptografische Design und die Entscheidungen, die für die Proof-of-Liabilities-Lösung von SwissBorg getroffen wurden, um ein besseres Verständnis dafür zu schaffen, warum und wie sie zustande gekommen ist.

Wenn dir dieser Artikel zu technisch ist, du aber trotzdem wissen willst, wie du deine Verbindlichkeiten überprüfen kannst, findest du weiter unten im Abschnitt "So kannst du deine Verbindlichkeiten überprüfen" die entsprechenden Schritte.

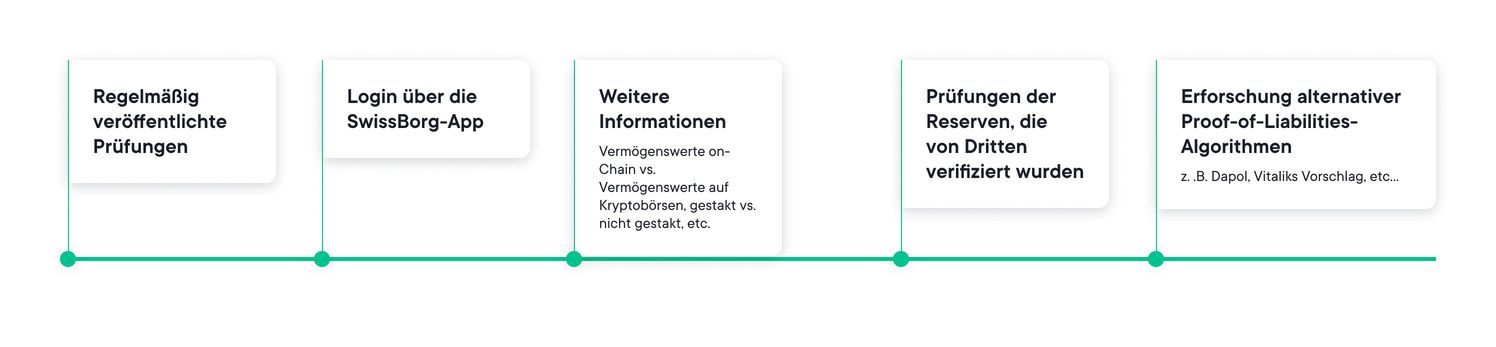
Unsere nächsten Schritte sind in dem folgenden Zeitplan dargestellt:

Die Grundlagen

Ein Proof-of-Liabilities-Dokument (PoL) oder -Dashboard verwendet ein Protokoll das zwischen einem Prüfer (“Prover”) und den Überprüfern (“Verifiers”) interagiert, um die Verbindlichkeiten zwischen den beiden aufzuzeigen. Es liegt auf der Hand, dass der Prüfer den Nachweis erbringt und der Überprüfer diesen Nachweis empfängt und auf seine Richtigkeit hin überprüft. In unserem Fall ist der Prüfer SwissBorg und die Überprüfer sind unsere Nutzer.

Verbindlichkeiten sind die Guthaben, die die Nutzer in ihren von SwissBorg verwalteten Wallets halten. Der Wert dieser Verbindlichkeiten bzw. Guthaben wird einfach durch eine positive Zahl dargestellt.

Das Hauptziel des PoL-Dienstes ist es, den Nutzern die Möglichkeit zu geben, zu überprüfen, ob ihre Guthaben in der Gesamtsumme der Verbindlichkeiten aller Nutzer enthalten sind. Im Wesentlichen bietet ein PoL die Gewissheit, dass der Prüfer die Verbindlichkeiten eines Nutzers nicht übersehen haben kann, indem er den PoL prüft.

Offenlegung von Verbindlichkeiten (Liabilities)

Die einfachste Methode zur Bereitstellung eines PoL ist eine, bei der das Unternehmen öffentlich zeigt, wie hoch die Guthaben der einzelnen Nutzer sind, so als ob man bei der Bank einen Kontoauszug mit den Guthaben aller Kunden vorlegen würde. Technischer ausgedrückt, zeigt der Prüfer eine Liste aller Überprüfer und ihrer Verbindlichkeiten. Aus dieser Liste müssen alle Informationen klar hervorgehen, sie muss öffentlich zugänglich sein und idealerweise dynamisch geführt werden, um alle Änderungen anzuzeigen.

In einem sehr vereinfachten Beispiel sehen wir ein Hauptbuch mit Konten, den zugehörigen Werten und der Gesamtsumme: Ein Hauptbuch, bei dem der Prüfer die Informationen für alle sichtbar und einsehbar gemacht hat und bei dem die Nutzer als Überprüfer fungieren, um sicherzustellen, dass die Informationen korrekt sind.

Alice: 9 USD

Bob: 6 USD

Carlos: 7 USD

Diana: 4 USD

---------------------------------

 Total: 26 USD

Bei diesem einfachen Beispiel sind einige wichtige Punkte zu beachten.

• Jeder Nutzer kann überprüfen, ob seine eigenen Verbindlichkeiten mit den aufgelisteten übereinstimmen und dass sich alle Verbindlichkeiten zum veröffentlichten Gesamtbetrag summieren.
• Wenn der Prüfer die Verbindlichkeiten des Nutzers weglässt oder falsch bereitstellt, ist der Prüfer eindeutig verantwortlich und trägt das Risiko, erwischt zu werden.
• Dieser elementare Ansatz erfüllt die Aufgabe, weist jedoch schwerwiegende Mängel auf, insbesondere in Bezug auf den Datenschutz.

Betrachtet man die spezifischeren Eigenschaften von PoL, zeigen die folgenden Themen die entscheidenden Eigenschaften, die im PoL-Prozess verwendet und den Überprüfern offengelegt werden müssen.

Privatsphäre

Die Offenlegung von Finanzinformationen mit entsprechenden Benutzeridentitäten ist eindeutig ein No-Go und nicht Teil unseres PoL-Berichts.

Unabänderlichkeit Ein weiteres potenzielles Problem ist die Formbarkeit der offengelegten Informationen. Tatsächlich kann der Prüfer verschiedenen Nutzern unterschiedliche Listen von Verbindlichkeiten anzeigen, um zu versuchen, den realen Wert der Gesamtheit der Verbindlichkeiten zu verringern. Um dies zu verhindern, müssen wir einen „öffentlichen Daten-Fingerabdruck“ einführen, der von jedem einzelnen Nutzer verifiziert werden kann, um sicherzustellen, dass alle denselben Datensatz erhalten haben. In der Informatik wird diese Art von Publikationsinfrastruktur mit dem Begriff Public Bulletin Board (PBB) bezeichnet.

Innerhalb des Themas der Unabänderlichkeit sind zwei zusätzliche Eigenschaften zu erwähnen, die durchgesetzt werden müssen:

Positives Guthaben

Ein Teil der Überprüfung der Summe der Guthaben der Nutzer ist, ob jedes Guthaben positiv ist. Es ist einem böswilligen Prüfer möglich, gefälschte Einträge hinzuzufügen, die keinem der Nutzer entsprechen, ohne Gefahr zu laufen, entdeckt zu werden.

Auch wenn der Prüfer diese falschen Einträge hinzufügen könnte, gäbe es für den Prüfer keinen Anreiz, dies zu tun, da dies nur die von ihm gehaltenen Verbindlichkeiten erhöhen würde. Aus Sicht der Nutzer würde sich lediglich ändern, dass der Prüfer weniger zahlungsfähig erscheint, als er tatsächlich war, sodass kein wirklicher Anreiz besteht.

Eindeutige Nutzerkennung

Wenn es eine öffentliche Offenlegung der Verbindlichkeiten aller Nutzer gibt, müssen natürlich alle einzelnen Verbindlichkeiten durch eine Kennung mit ihrem spezifischen Nutzer verknüpft werden. 

Innerhalb dieses Themas gibt es einen schelmischen Schachzug, den der Prüfer machen könnte. Unter der Annahme, dass zwei verschiedene Nutzer genau das gleiche Guthaben hatten, könnte ihnen beiden dieselbe Kennung zugewiesen werden, beide würden derselbe „Nutzer“ mit demselben Inklusionsnachweis, was es SwissBorg ermöglicht, die Summe an der Spitze des Merkle Trees effektiv zu verringern. Wir würden beide Nutzerguthaben nur einmal abrechnen.

In unserem System verwenden wir eine Benutzer-ID, die einzigartig ist und daher für jeden Benutzer anders aussieht. Es handelt sich dabei um die Benutzer-ID, die sich bereits in der SwissBorg-App befindet.

SwissBorgs Proof-of-Liabilities

Designauswahl auf hohem Niveau 

Das spezifische Design des Proof-of-Liabilities-Services von SwissBorg ist das Ergebnis der Verwendung bestehender State-of-the-Art-Methoden, die an unsere spezifischen Anforderungen angepasst wurden: Mehrere Währungen, In-Browser-Verifizierung, kein externer Prüfer, gepaart mit einer Notwendigkeit für eine schnelle Implementierung und Durchsetzung.

Bei der Analyse der vorhandenen Literatur zu PoL-Protokollen wurde deutlich, dass wir die Wahl zwischen zwei Hauptoptionen hatten:

• Basierend auf dem Standard-Merkle Tree
• Basierend auf fortgeschrittener Kryptografie (z. B. zk-snarks)

Die erste Wahl eines auf dem Merkle Tree-basierenden Standardansatzes leitet sich von etablierten kryptografischen Primitiven ab, die in fast jeder Programmiersprache problemlos implementiert werden können, während die letzteren auf fortgeschrittener Kryptografie basierenden Protokolle die Verwendung von „Nischen“ und fortschrittlichen kryptografischen Bibliotheken viel größere Implementierungsbemühungen erfordern würden.

Um die Entscheidung weiter zu unterstützen, macht die Verwendung gut verstandener und einfacher kryptografischer Grundelemente das Ergebnis weniger fehleranfällig. Aus diesem Grund basiert unser PoL-Design auf der Merkle Tree-Linie, die durch den Maxwell-Todd-Vorschlag von 2013 initiiert wurde, wie er von Gregory Maxwell und Peter Todd präsentiert wurde. Wir haben die vorhandene Literatur und Arbeitsimplementierungen studiert, um die neuesten Verbesserungen zu nutzen.

Wer ist Merkle und warum hat er einen Tree (Baum)?

Kryptografische Hash-Funktionen sind der Kernbestandteil zahlreicher kryptografischer Protokolle. Ein Hash, für den Unwissenden, ist eine Funktion, die eine Eingabe beliebiger Größe aufnimmt und eine kleine Ausgabe fester Größe zurückgibt. In einem vereinfachten Beispiel wird eine Eingabe von „Satoshi“ die 4-stellige 2341 ausgeben, und die Eingabe des gesamten Textes des ersten Buches von Harry Potter wird auch nur die 4-stellige Ausgabe von 7654 ergeben. 

Hashes liefern Ausgaben gleicher Länge von Eingaben unterschiedlicher Länge, und die Ausgabe kann nicht auf die Eingabe zurückgeführt werden. Aufgrund dieser Funktion ist diese Ausgabe, auch „Hash“ genannt, ein rechnerisch eindeutiger Fingerabdruck ihrer Eingabe.

Wenn du dann einen Hash des Hashs nimmst, beginnt sich eine Struktur zu bilden, die mit jeder Iteration kleiner wird und Blättern, Zweigen und einem Stamm ähnelt. Im weiteren Verlauf dieser Sequenz können die Daten an keinem Punkt des Prozesses  geändert werden oder alle nächsten Hashes würden sich ebenfalls ändern, was zu einer Struktur führt, in der die Eingabedaten vor Änderungen geschützt sind.

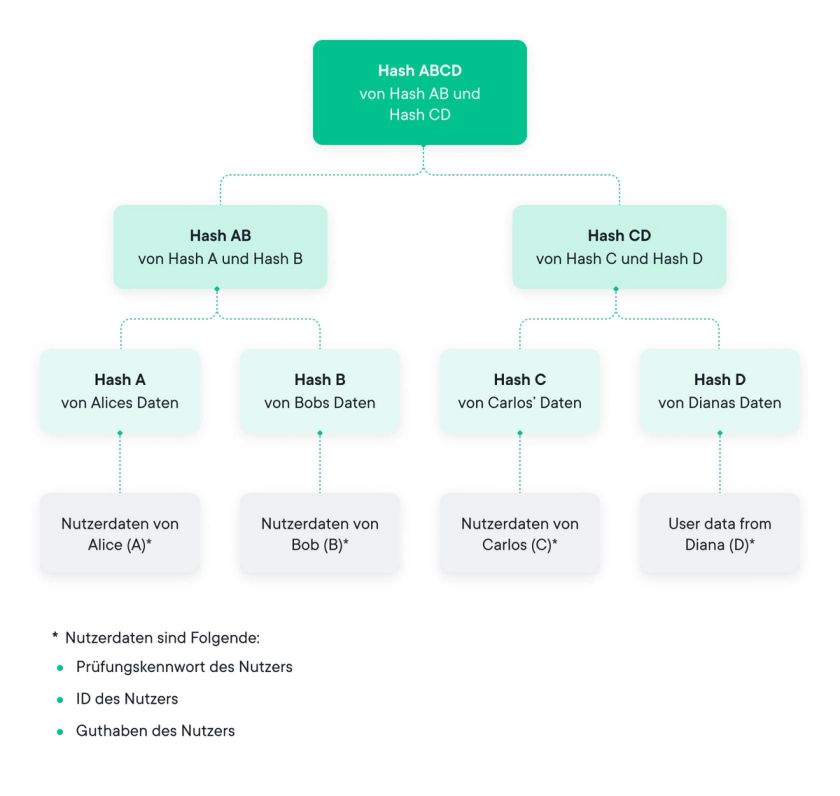
Die Einführung des Merkle Tree geht auf die Erfindung der Public-Key-Kryptographie Ende der 1970er Jahre zurück und ist nach seinem Erfinder Ralph Merkle benannt. In seiner einfachsten Form besteht ein Merkle Tree aus einer binären baumähnlichen Datenstruktur, bei der jedes Blatt der Hash eines Datenblocks und jeder Parent Node der Hash beider Child Hashs ist:

Hparent = Hash ( HA | | HB ) [wenn HA und HB entsprechende Child Hash-Werte sind]

Oben enthält das Wurzel-Element (und ja, wir wissen, dass Baumwurzeln am unteren Ende des Baums im Boden sind) einen Hash, der im Wesentlichen alle zugrunde liegenden Daten zusammengefasst hat.

Aufgrund der zugrunde liegenden Eigenschaften von Hash-Funktionen ist es unmöglich, die Daten an irgendeiner Stelle des Trees zu ändern, ohne den Wurzel-Hash-Wert zu ändern. Wenn etwas geändert wird, ändert sich der Rest der Struktur. Bisher unterscheidet sich das nicht sehr vom Hashing aller Daten. Der Merkle Tree ermöglicht es uns jedoch, eine große Anzahl von Dateneingaben – auch als Blöcke bezeichnet – auf eine Weise zusammenzufassen, die sehr effizient ist, um die Einbeziehung eines bestimmten Datenblocks zu überprüfen.

Anders ausgedrückt, diese Verifizierungsmethode kann verwendet werden, um zu zeigen, dass ein bestimmter Datenblock in den Tree aufgenommen wurde und dass sich dieser Block auf dem Pfad der nachfolgenden Geschwisterknoten (auf dem „Inklusionspfad“) bis zum Wurzel-Hash befand. Aus diesem Grund wird die Größe des Inklusionsnachweises logarithmisch statt linear. Für 1 Million Blätter enthält der Beweis also nur 20 Knoten, den Wurzelknoten nicht eingeschlossen.

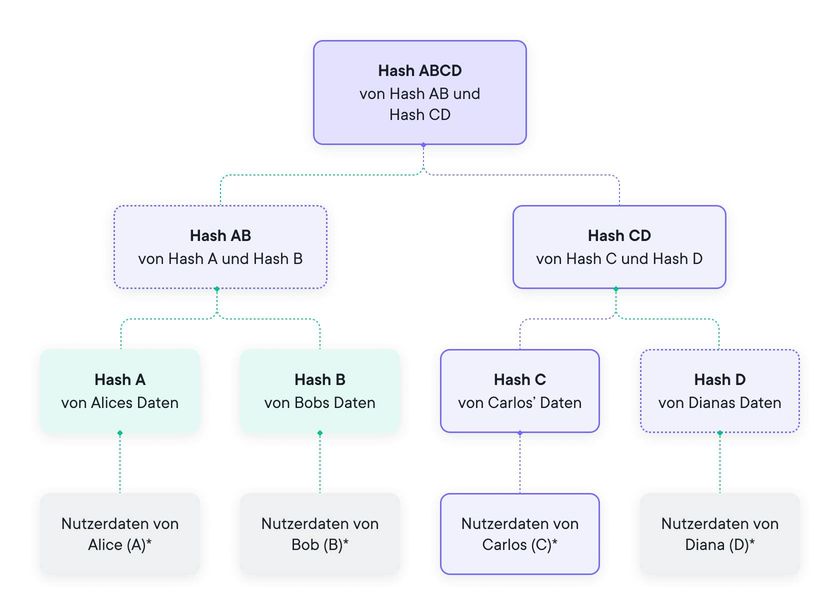
An der Spitze des Trees fungiert dieser Wurzel-Hash-Wert als Commitment-Verfahren, da die zugrundeliegenden Daten nicht mehr geändert werden können, sobald dieser Wert angezeigt wird. Auf der anderen Seite dieser Münze ist es unmöglich zu behaupten, dass Daten enthalten waren, die nicht beim Bau des Merkle Trees vorhanden waren, da alles sichtbar ist und nicht manipuliert werden kann.

Die Maxwell-Todd-Linie von PoL

Wie oben erwähnt, wird Maxwell-Todd im Jahr 2013 der erste Vorschlag für PoL auf der Grundlage eines Merkle Trees zugeschrieben. Ihr Vorschlag basierte auf der Verwendung eines Merkle Trees mit Datenblöcken, die das Guthaben eines Nutzers enthielten. Zusätzlich wird jeder Knoten dieses Merkle Trees um eine Verbindlichkeit erweitert, die sich aus der Summe aller Verbindlichkeiten der jeweiligen untergeordneten Knoten zusammensetzt. Aus diesem Grund besteht jeder Knoten aus einem Digest und einer positiven Bilanz.

Auf diese Weise wird der Saldo des Root Node zur Summe aller Nutzerverbindlichkeiten. Diese Datenstruktur wird als "Summation Merkle Tree" ("Summen-Merkle Tree") bezeichnet, wie im nachstehenden Diagramm dargestellt wird.

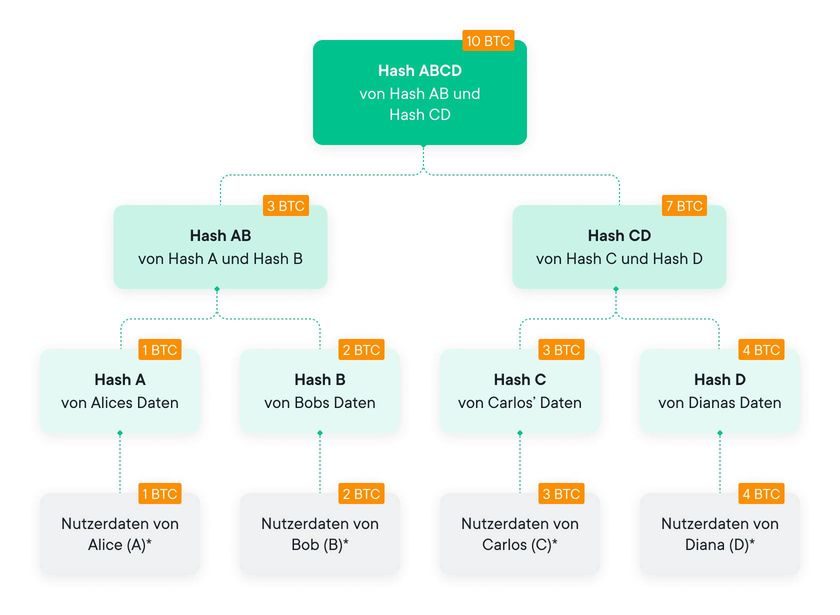
Hier wird es nun interessant. Der Hash-Wert eines Blattknotens wird durch Hashing der ID eines Nutzers, der Anmeldeinformationen und des Kontostands des Nutzers erhalten. Die Zugangsdaten des Nutzers dienen dazu, die Nutzer-ID zu maskieren, um die Privatsphäre des Nutzers zu schützen. Um die Sicherheit dieses Verfahrens zu verbessern, wird die Position des Blattknotens eines bestimmten Nutzers zufällig ausgewählt, um die Verbindung zwischen einem Nutzer und seinem Guthaben zu unterbrechen. Der Hash-Wert jedes anderen Knotens wird berechnet, indem die Verbindlichkeiten der untergeordneten Knoten und ihre jeweiligen Digest-Werte gehasht werden.

Hparent = Hash ( BalA | | BalB | | HA | | HB )

Um einem Nutzer zu zeigen, dass seine Verbindlichkeiten im Merkle Tree enthalten sind, stellt der Prüfer einen Inklusionspfad bereit. Dies geschieht auf die gleiche Weise wie bei einem Standard-Merkle Tree, nur erweitert um die Liability-Summe.

Bei der Validierung berechnet der Nutzer den Parent Hash wie oben und überprüft dann die Summe der Child Hash-Guthaben. Als Teil dieser Summationsprüfung überprüft der Nutzer auch, dass sowohl BalA als auch BalB positiv sind und dass BalA + BalB = Bal ist, wobei BalA, BalB die Salden der Child Hash und Bal die Verbindlichkeit des Parent Hashs sind. Dieser Validierungsschritt wird auf jeder Ebene des Merkle Tree durchgeführt, von den Blättern bis zur Wurzel.

Wir stellen fest, dass der obige Summation Merkle Tree einer leicht modifizierten Version des ursprünglichen Merkle Trees von Maxwell Todd entspricht, aufgrund der Anwendung der Erkenntnisse, die in einer wissenschaftlichen Arbeit von Hu, Zhang, and Guo (2019) präsentiert wurden, die eine Sicherheitslücke behebt. Die neue Variante des Merkle Trees wurde mit dieser Sicherheitslückenkorrektur aktualisiert und in einer wissenschaftlichen Arbeit von Ji-Chalkias (2021) als „Maxwell+Merkle-Tree" geprägt; der Name ist hängengeblieben.

In Fortsetzung dieser logischen Linie wird in der Arbeit von Ji-Chalkias (2021) eine Methode erwähnt, um ursprüngliche Nutzerguthaben zu verbergen, indem jedes in mehrere Shards aufgeteilt wird – eine Erkenntnis, die Chalkias, Lewi, Mohassel, and Nikolaenko im Jahr 2019 zugeschrieben wird – und gemischt wird sie zufällig in den Baumblättern. Der Logik der Nomenklatur folgend, wurde diese nächste Variante von Ji-Chalkias (2021) Maxwell++Merkle-Tree genannt.

Zusammenfassend können wir sagen, dass der Fortschritt dieser kryptografischen Methode für den praktischen Einsatz bei Haftungsnachweisen mit der Iteration von Maxwell-Todd erfolgte, bei der der Merkle Tree Summierung enthalten konnte. Auf der Zeitachse der Innovation wurde eine Sicherheitslücke gefunden und behoben, die zur Einrichtung und Verwendung der Maxwell+-Variante führte, und die endgültige Version, in der das Guthaben jedes Nutzers in Shards aufgeteilt wurde, um die tatsächlichen Nutzerverbindlichkeiten zu verschleiern, führte zu Maxwell++. Jede dieser Verbesserungen war wichtig und wurde von der Community begrüßt. Wir freuen uns, diese Technologie auch in unserer Lösung einzusetzen.

SwissBorgs Design-Wahl

Da die SwissBorg-Plattform mehr als 70 Fiat- und Kryptowährungen unterstützt, besitzen die Nutzer in der Regel eine Reihe davon. Im Prinzip könnten wir einen einzigen Merkle Tree anwenden, um alle Währungen gleichzeitig abzudecken, indem wir die Summe der Salden währungsmäßig anwenden. Für viele Nutzer ist die Aufschlüsselung der Währungen in ihrem Portfolio jedoch einzigartig und würde daher ein ernstes Datenschutzproblem darstellen.

Als Abhilfe behandelt unser Design jede Währung separat, da wir einen dedizierten Merkle Tree für jede Währung erstellen. Wir sammeln dann alle Stammdaten des Merkle Tree zu einem sogenannten Audit Commitment Hash, der der Hash-Wert aller Währungsverbindlichkeiten und der jeweiligen Stamm-Hashes des Trees ist.

Im Wesentlichen kann die gesamte Konstruktion als ein einziger Merkle Tree angesehen werden, mit dem Unterschied, dass die obere Schicht aus so vielen Zweigen besteht wie die Anzahl der Währungen. Aufgrund dieser Eigenschaft müssen zur Überprüfung der Verbindlichkeiten alle Währungswurzeln des Merkle Trees als Teil des Inklusionsnachweises gesendet werden.

Um die Privatsphäre der Nutzerguthaben weiter zu verbessern, teilen wir jedes Nutzerguthaben in mindestens 2 positive Unterguthaben/Shards auf, und ihre Positionen in den Blättern des Merkle Trees werden nach dem Zufallsprinzip bestimmt. Der Einfachheit halber und um die Anzahl der Nutzer pro Währung teilweise zu verbergen, generieren wir immer eine Anzahl von Unterbilanzen gleich der Potenz von 2, damit der binäre Merkle Tree vollständig ist.

Es ist erwähnenswert, dass die Aufteilung der Guthaben mit der PoL-Lösung von Bitmex und der Maxwell++-Variante mit einem Aufteilungsfaktor > 2 übereinstimmt.

Gemäß dem Maxwell++-Design wird die Privatsphäre der Nutzer erreicht, indem einige High-Entropy-Masking-Nonces in die Blattdaten aufgenommen werden. Anhand eines Blattknotens – Hash und Guthaben – ist es nicht möglich, die entsprechende Nutzeridentität herauszufinden. Diese sogenannte „Blatt-Nonce“ wird von einem Audit-ID pro Nutzer abgeleitet, bei dem es sich um einen 128-Bit-Zufallswert handelt, der ausschließlich für die Zwecke des PoL bestimmt ist. 

Wo finde ich meine Kredenzien?

Deine Zugangsdaten findest du im Sicherheitsregister der SwissBorg-App. Wir haben es „Prüfungskennwort“ genannt, um zu betonen, dass Nutzer es vertraulich behandeln müssen, da jemand sie verwenden könnte, um die Guthaben des Nutzers offenzulegen – mit entsprechenden Blattknoten.

Das Prüfungskennwort soll langfristig aufbewahrt und über mehrere Instanzen von Haftungsnachweisprüfungen wiederverwendet werden. Nach kryptografischen Standardpraktiken werden die Blatt-Nonces – mit einer kryptografischen Schlüsselableitungsfunktion – auf hierarchische Weise abgeleitet:

• Audit-ID, Nutzer-Prüfungskennwort → Audit Nonce
• Audit Nonce, Währung → Merkle-Tree Nonce
• MT Nonce, Blattindex → ​​Nonce des Blattknotens
• Blattdaten: Blatt-Nonce, Benutzer-ID, Balance-Shard

Ein weiteres wichtiges Detail ist, dass diese unterschiedlichen Ebenen von Nonces verwendet werden können, um Informationen in Bezug auf die Nutzerverbindlichkeiten mit unterschiedlichen Besonderheiten offenzulegen, beispielsweise pro Prüfung oder pro Währung.

Natürlich braucht jeder eine Nutzerkennung, und dafür haben wir uns für die SwissBorg-Benutzer-ID entschieden, die an allen Stellen des Prozesses mit ihrem Nutzer verknüpft ist und in der App ganz einfach unten auf der Registerkarte Profil gefunden werden kann in Form von:: 20XXX. Diese Kennung ändert sich nie und ist für jeden Nutzer eindeutig.

Der PoL-Dienst von SwissBorg bietet mehrere Merkle Tree-Inklusionspfade, einen Subbalance-Shard pro Nutzer, der durch ein im Browser ausgeführtes Skript validiert wird und die Gesamtsalden für diesen Nutzer wiedergibt.

Die Validierungsprüfung wird in Bezug auf die Prüfverpflichtungs-Hashes durchgeführt, die über Twitter veröffentlicht werden. Der Algorithmus lässt sich wie folgt zusammenfassen:

1. Alle Merkle-Stammknoten werden gegen den „Audit Commitment Hash“ geprüft. Außerdem kann der Nutzer überprüfen, ob dieser Hash mit dem auf Twitter veröffentlichten übereinstimmt.
2. Für jeden Inklusionspfad wird der Pfad validiert, indem der Parent Node rekursiv mit dem Geschwisterknoten berechnet wird, der durch den Inklusionsnachweis bereitgestellt wird, und verifiziert, dass der oberste Knoten einem der Wurzelknoten des Merkle Trees entspricht, die im vorherigen Schritt validiert wurden. Als Teil dieses Prozesses wird für jeden Child Hash eine Prüfung durchgeführt, um sicherzustellen, dass sie positive Verbindlichkeiten haben.
3. Nach jeder erfolgreichen Inklusionsnachweisvalidierung wird das entsprechende Nutzerblattguthaben zu den Gesamtverbindlichkeiten des Nutzers hinzugefügt.
4. Wenn kein Fehler aufgetreten ist, werden die gesamten Verbindlichkeiten des Nutzers zurückgegeben.

Diskussion

Das SwissBorg Proof-of-Liabilities-Design basiert auf einer hochmodernen Merkle-Tree-basierten Konstruktion, die die größtmögliche Vertraulichkeit der Nutzeridentitäten und der damit verbundenen Verbindlichkeiten gewährleistet. Darüber hinaus haben wir uns entschieden, die einfache Bedienung und die vom Nutzer durchgeführte Selbstverifizierung zu betonen, was bedeutet, dass im Gegensatz zu mehreren anderen Proof-of-Liabilities-Lösungen, beispielsweise der von Kraken, kein externer Prüfer beteiligt werden muss.

Unser Ansatz entspricht eher der Wahl von Bitmex, mit dem Hauptunterschied, dass unsere Überprüfung leichter ist und eine Einstellung für mehrere Währungen ermöglicht.

Diese leichtgewichtige Eigenschaft ergibt sich aus der Tatsache, dass der Nutzer keinen vollständigen Merkle Tree herunterladen muss, sondern nur Inklusionsnachweise, die einen kleinen Bruchteil des Trees darstellen. Dies ermöglicht eine In-Browser-Validierung, die vom Nutzer eingesehen werden kann, wenn er dies wünscht.

Wir sind zu dem Schluss gekommen, dass die Nichtveröffentlichung des vollständigen Merkle Trees keineswegs eine Schwachstelle darstellt, da der Audit Commitment Hash die Integrität der zugrunde liegenden Daten garantiert – es ist kryptografisch unmöglich, Daten im Merkle Tree nachträglich zu ändern.

Die Offenlegung des vollständigen Merkle Trees kann nur garantieren, dass die Struktur wohlgeformt ist, in dem Sinne, dass alle Verbindlichkeiten positiv sind und die Hashes der Nicht-Blatt-Knoten korrekt sind.

Einschränkungen

In Bezug auf Einschränkungen kann ein Nutzer, der die Validierung durchführt, nicht erkennen, ob eine Liability eines anderen Nutzers falsch ist oder weggelassen wurde. Um einen Fall von Manipulation durch einen böswilligen Anbieter aufzudecken, ist eine Validierung durch die betroffenen Nutzer erforderlich, unabhängig vom vollständigen Merkle Tree oder der Offenlegung von Einschlussnachweisen.

Sowohl die Zusicherung, dass die Gesamtzahl der Liabilities als auch der Gesamtwert nicht vom Anbieter herabgesetzt wurden, hängt vom Grad der Beteiligung der Nutzer ab. 

Mit diesem Nicht-Drittanbieter, nur einschlusssicheres Selbstverifizierungssystem, je mehr Nutzer ihre Liabilities überprüfen, desto besser. Dies liegt daran, dass je mehr Menschen sich die Informationen ansehen, desto größer ist die Wahrscheinlichkeit, dass, wenn etwas nicht stimmt, es gesehen wird, und der Nutzerkonsens größer wird.

Dies läuft auf das Grundkonzept hinaus: "Je mehr Leute etwas überprüfen, desto geringer ist die Wahrscheinlichkeit, dass der Prüfer daran herumspielen kann und nicht bemerkt wird".

In Abschnitt 5 der zuvor erwähnten wissenschaftlichen Arbeit von Ji-Chalkias stellen die Autoren eine detaillierte Berechnung vor, wie viele Nutzer, die Inklusionsnachweise durchführen, erforderlich sind, um ein Fehlverhalten seitens des Prüfers zu erkennen.

Es gibt zusätzliche Einschränkungen bei unserer Lösung, die keine Bedrohung für die Sicherheit darstellen und ständig verbessert werden. Diese Einschränkungen beziehen sich auf:

• einige Informationen zu einzelnen Liabilities– ohne Verknüpfung mit Nutzerkennungen,
• die Privatsphäre der Anzahl der Nutzer pro Währung,
• die Gesamtverbindlichkeiten.

Unserer Ansicht nach wurde die erste auf der Liste – die Einschränkung des Datenschutzes bei Informationen zu einzelnen Verbindlichkeiten – mit unserer Lösung durch „Splitting von Salden“ gelöst, die immer noch Teilinformationen anzeigt, wie z. B. die Angabe, ob ein Saldo einen bestimmten Betrag übersteigt, aber nicht persönliche Daten.

Zur Verdeutlichung:  Das Aufteilen von Salden bedeutet lediglich, dass das ursprüngliche Nutzerguthaben in Teilguthaben zerlegt wird, sodass die Summe der Teilguthaben = das ursprüngliches Guthaben ist. Dadurch erscheint das ursprüngliche Gleichgewicht nicht im Merkle Tree.

Die zweite und dritte Einschränkungen beziehen sich eher auf Informationen, die der Anbieter möglicherweise privat halten möchte und die kein echtes Datenschutzrisiko für unsere Nutzer darstellen. Die gute Nachricht ist, dass an modernen Lösungen gearbeitet wird, die auf fortschrittlicheren kryptografischen Konstruktionen wie zk-SNARKS basieren, die diese Probleme lösen und uns in Zukunft die Möglichkeit geben, Einschränkungen noch weiter zu implementieren und zu reduzieren.

Im Moment sind diese Lösungen aufgrund ihrer Neuheit weniger zugänglich und erfordern mehr Entwicklung von unserer Seite. Aus diesen Gründen haben wir uns entschieden, zunächst die bewährte Merkle-Tree-Lösung zu implementieren, da die verbleibenden Einschränkungen nicht kritisch sind.

Wir behalten all diese Lösungen im Auge, einschließlich des viel diskutierten Vorschlags von Vitalik und der bereits erwähnten sehr vielversprechenden Dapol+-Lösung von Ji-Chalkias, die erstmals die Aufmerksamkeit der kryptografischen Community auf der Computer and Communications Security Conference, ACM CCS 2021, auf sich zog. Wir werden unsere Lösung weiter erneuern und Verbesserungen integrieren; immer innovativ voraus.

Warum keine externen Prüfer? 

Obwohl die Nutzerselbstverifizierung eine strikte Anforderung unseres Systems war, schließt dies nicht die Möglichkeit der Einbeziehung eines externen Prüfers in Zukunft aus. Einer der potenziellen Vorteile, einen an Bord zu haben, besteht darin, die Erkennungsfähigkeit zu erhöhen und sich nicht nur auf die Beteiligung der Nutzer zu verlassen, um einen betrügerischen Anbieter zu erkennen.

Einige gute Beispiele für diesen positiven Einfluss sind die folgenden:

• Ein externer Prüfer könnte systematisch einige Stichproben von Nutzerverbindlichkeiten anhand des Proof-of-Liabilities überprüfen.
• Beteiligung eines Prüfers im Falle einer Streitbeilegung, bei der ein Nutzer falsche oder fehlende Verbindlichkeiten im Haftungsnachweisbericht geltend macht.

Es scheint, als wäre ein solches Problem nur mit technischen Mitteln schwer zu lösen, und die Einbeziehung eines externen Prüfers könnte sehr hilfreich sein. Um diesen Punkt zu vertiefen, geht er in der Sicherheitsanalyse von Chalkias von Binance PoL auf die Tatsache ein, dass die Beteiligung eines Prüfers den Anbieter daran hindern könnte, Nutzer zu verfolgen, die die Überprüfung durchführen, und die Haftung gegenüber denjenigen, die dies nie überprüfen, ausschließen könnte. Alles Dinge, die für zukünftige Iterationen zu berücksichtigen sind.

So wird validiert

Als Nutzer kannst du deine Verbindlichkeiten überprüfen und validieren, indem du die “Sicher mit SwissBorg”-Seite auf unserer Website besuchst.

Bitte folge den Anweisungen auf der Seite und gib deine  personalisierte Nutzer-ID ein, die du im Abschnitt Sicherheit der SwissBorg-App findest.

Es ist wichtig zu wissen, dass die Verbindlichkeiten, die du sehen wirst, zum Zeitpunkt der letzten Prüfung übernommen wurden und daher keine „Live“-Darstellung deiner Verbindlichkeiten sind. Diese Audits sollen regelmäßig stattfinden, wobei die Häufigkeit noch bekannt gegeben wird, sobald sie endgültig festgelegt ist.

Wenn du mit dem Begriff „GitHub-Repo“ vertraut bist und deine Verbindlichkeiten lokal auf deinem Computer überprüfen und validieren möchtest, folge bitte den Anweisungen im veröffentlichten Quellcode SwissBorg Proof-of-Liabilities Repo.

Abschließende Bemerkung

Der Nachweis, was wir für unsere Nutzer halten, ist im Krypto-Bereich zur Standardpraxis geworden, und wir sind stolz darauf, unabhängig eine Lösung entwickelt zu haben, die den Nutzern die Möglichkeit bietet, ihre Bestände zu überprüfen.

Die erste Version des SwissBorg-Portals für Proof-of-Liabilities wurde veröffentlicht, die es jedem Nutzer ermöglicht, seine entsprechenden Verbindlichkeiten einfach zu validieren, ohne sich auf externe Prüfer verlassen zu müssen, und gleichzeitig ein hohes Maß an Sicherheit und Datenschutz erreicht.

Dies ist eine fortlaufende Initiative und wir behalten mögliche Entwicklungen im Auge. Insbesondere könnten wir erwägen, eine der fortgeschritteneren kryptografischen Techniken zu implementieren, um die Stärke des Systems zu verbessern, wie Vitaliks Vorschlag, wenn es soweit ist.

Sichere, offene, Nutzerfreundliche und Nutzerzentrierte Beweise ist ein entscheidendes Thema, an dem viele kluge Köpfe und aus verschiedenen Perspektiven gearbeitet wird. Davon abgesehen kann es eine Weile dauern, bis sich die Branche der Standardisierung von PoL nähert, aber wir sehen dies als eine positive Unvermeidlichkeit für alle.

Im Moment zählt jedoch jeder auf jeden, was bedeutet, dass wir uns darauf verlassen, dass unsere großartigen Nutzer sich einen Moment Zeit nehmen und ihre Verbindlichkeiten über das Proof-of-Liabilties-Portal validieren und dabei wissen, dass sie nicht nur ihre Krypto-Assets sichern und nachweisen, sondern auch zur Stärkung des Vertrauens in SwissBorg und unsere großartige Community beitragen.

Haftungsausschluss

Bitte beachte, dass die Informationen zu den Verbindlichkeiten der Nutzer, die in unserem Protokoll zum Nachweis der Verbindlichkeiten enthalten sind, im internen Hauptbuchsystem von SwissBorg erfasst werden. SwissBorg haftet nicht für falsch angegebene Salden, die sich aus einem Fehler oder Irrtum im Hauptbuch ergeben. Es liefert keine Informationen über andere Verbindlichkeiten oder Risiken des Unternehmens. Dieser Artikel ist nur für allgemeine Orientierungs- und Informationszwecke bestimmt und stellt kein öffentliches Angebot von virtuellen Vermögenswerten oder Finanzinstrumenten, keine Finanz- oder Anlageberatung oder irgendeine andere Art von Beratung dar und sollte nicht als irgendeine Form von Werbung, Empfehlung, Aufforderung, Angebot oder Befürwortung (i) zum Kauf oder Verkauf eines Produkts, (ii) zur Durchführung von Transaktionen oder (iii) zur Vornahme einer anderen rechtlichen Transaktion ausgelegt oder verstanden werden. Weder die SwissBorg Solutions OÜ noch die mit ihr verbundenen Unternehmen geben eine Garantie für die Vollständigkeit, Genauigkeit, Aktualität oder Eignung der in diesem Artikel enthaltenen Informationen oder dafür, dass diese fehlerfrei sind.